• [COM503] Deep Learning — Swiss Institute of Artificial Intelligence (siai.org)

Model examination is available from above link. The last class solves previous year's (or similar) exam while covering key components of the earlier classes.

Generative models are simply repeatedly updated model. Unlike discriminative models that we have learned from all previous lectures, such as linear/non-linear regressions, SVM, tree models, and Neural Networks, Generative models are closely related to Bayesian type updates. RBM (Restricted Boltzmann Machine) is one of the example models that we learned in this class. RNN, depending on the weight assignment for memory, can qualify generativeness.

To further help you to understand the difference, let's think about K-means. Once you have a fixed group, there is not much we can do, unless we run the same code to find another matching group. Then, what if there is a point that is nearly arbitrary to claim either group A or B. We may assign 50:50 probability, but K-means does not support such vagueness. Gaussian Mixture Model (GMM), however, assumes that there are N number of gaussian processes in the data, so a point at an overlapping area between group A and B can earn some probability (in terms of Z-stat) for its group assignment. The grouping is updated recursively, which qualifies generativeness.

With some Bayesian type updating between Prior and Posterior, we term them as EM algorithm.

• E-step: Compute the posterior probability that each Gaussian generates each datapoint
• M-step: Assuming that the data really was generated this way, change the parameters of each Gaussian to maximize the probability that it would generate the data it is currently responsible for

Like we did with Gibbs sampling (and RBM), the model eventually converges as long as it fits all mathematical properties.

The same process can be applied to any data that we don't know the hidden forms of underlying distribution and target distribution. For example, Latent Dirichlet Allocation (LDA), one of the most fundamental and popular natural language model, assumes that words in paragraphes have hidden variables, which it calls 'topic'. Simply put, each paragrah should have a few topics, but until one reads the paragraph carefully, it is not easy to capture the topics. LDA, with a vague assumption of the hidden variables, without any deterministic density information of words, finds hidden topics. The topics help us to find what are the contents of the paragraph, the section, and the book.

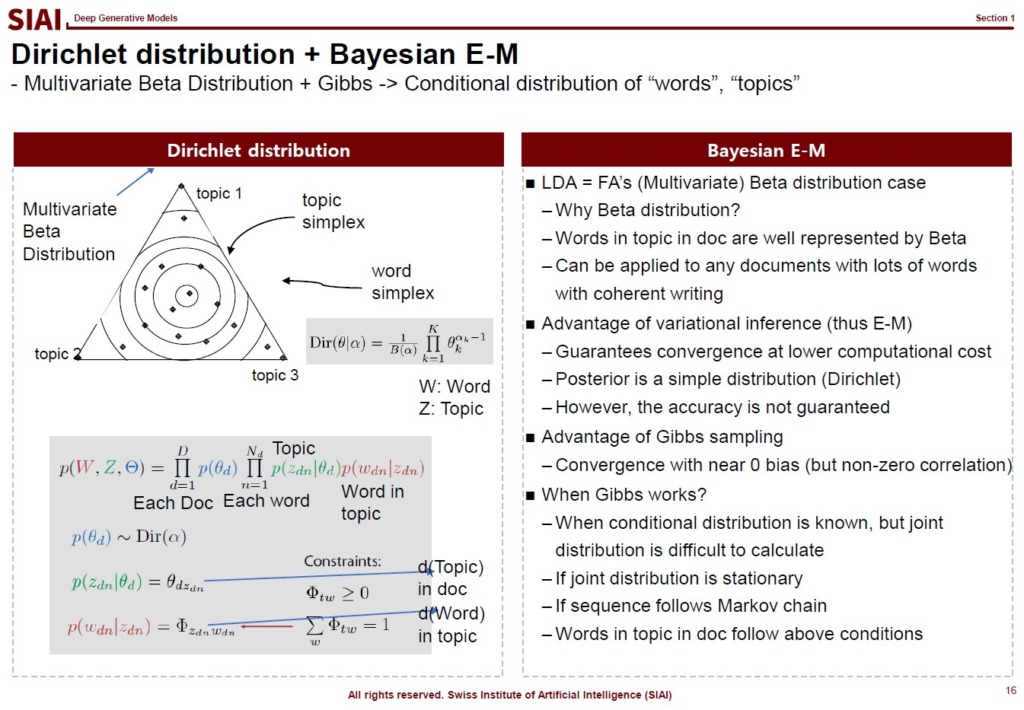
From autoencoder to GMM and LDA, due to interdependency between the input and output layers of network, all neural network models need some level of generative construction process, unless the universally fitted form of network is known.

It may sound too cumbersome, especially for researchers from analytic solutions, but the data that we have is highly irregular that we often have to rely on computational solutions.

Recurrent Neural Network (RNN) is a neural network model that uses repeated processes with certain conditions. The conditions are often termed as 'memory', and depending on the validity and reliance of the memory, there can be infinitely different variations of RNN. However, whatever the underlying data structure it can fit, the RNN model is simply an non-linear & multivariable extension of Kalman filter.

Given that NN models are just an extension of Factor Analysis for non-linear & multivariable cases with network structure, Kalman filter to RNN follows the same logic. The Kalman filter process updates previous state's variables after an observation and potential errors. Say, one can predict a car to move from position A to B. But in reality, you maybe able to find the car in position D. The error, e=(D-B), should be used to fix the model's next stage prediction. Assume that you give 50% weight to the error correction, because the error is not always that large. Then, the updated model will give the expected position C=B+0.5e. In other words, in every stage, previous stage's error helps correction so that we can hopefully minimize errors in later stages.

Then, we can see two aspects of RNN is just another combination of traditional stat models. From autogressive processes, we can see that memory is preserved. It does not mean that memory is completely preserved (like LSTM, a variation of RNN), but ARMA keeps memory to some distant future.

The error correction part by the state variable is similar to Kalman filter. RNN uses the state variable whether to turn on memory or skip it. When it turns on memory, depending on the choice of weights, the model reflects proportional amount of memory with some correction by the new input. In Kalman, it is called weighted error correction, like we end up with C, instead of B or D. In RNN, it is just feed forward and back propagation.

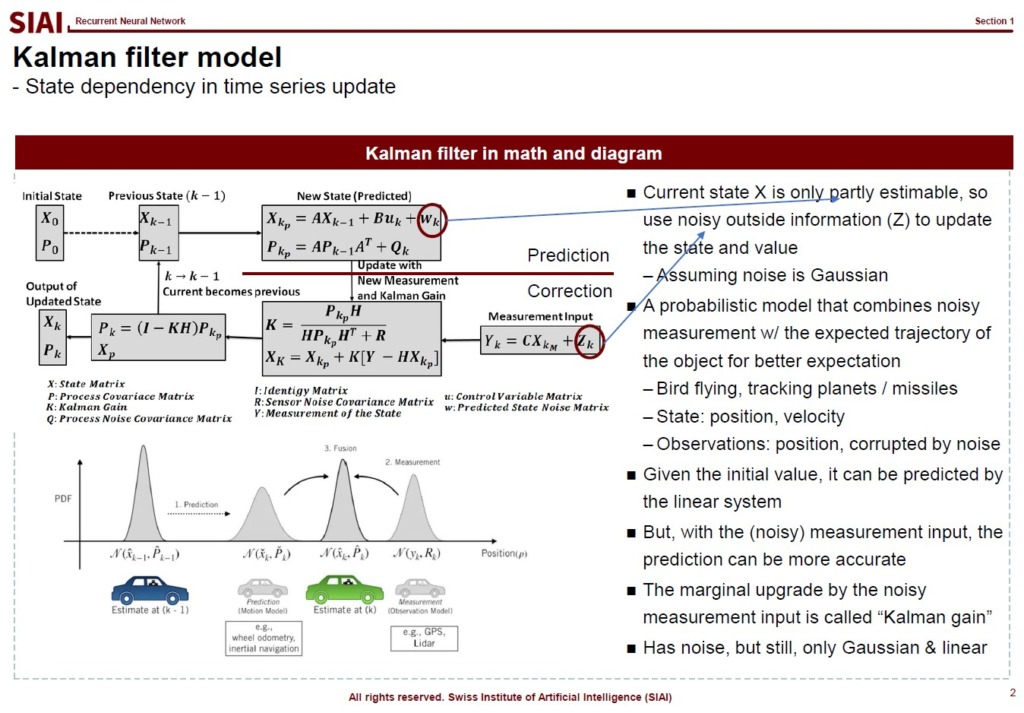
The reason RNN can perform superior to many time series processes with memory is due to its power to fit to non-linear and multivariable cases. Below is an equational form comparison between Kalman filter and RNN that illustrates the spectacular similarity in functional forms, except non-linear transformation like activation function.

Although one can construct a non-linear Kalman filter and even include more than one variable, but then VAR(Vector AutoRegressive) models are required with fixed functional form. RNN, on the other hand, relies more on data. Though the dependency to data creates similar problems that we have seen with other regular NN models, additional computational costs for certain data processes can be decently compensated for the better fit and flexibility.

As shown by RBM's autoencoder versions, if the neural network is well-designed, it can perform better than PCA in general when it comes to finding hidden factors. This is where image recognition relies on neural network.

Images are first converted to a matrix with RGB color value, (R, G, B), entries. The matrix is for the coordination of each RGB color value. If three dimensional image, then you need a tensor with RGB color value entries. In below sample, I took the average value of RGB entries for better understanding. In fact, if it is black/white, you only need the matrix, because (R, G, B) can be translated to a single 0~1 value.

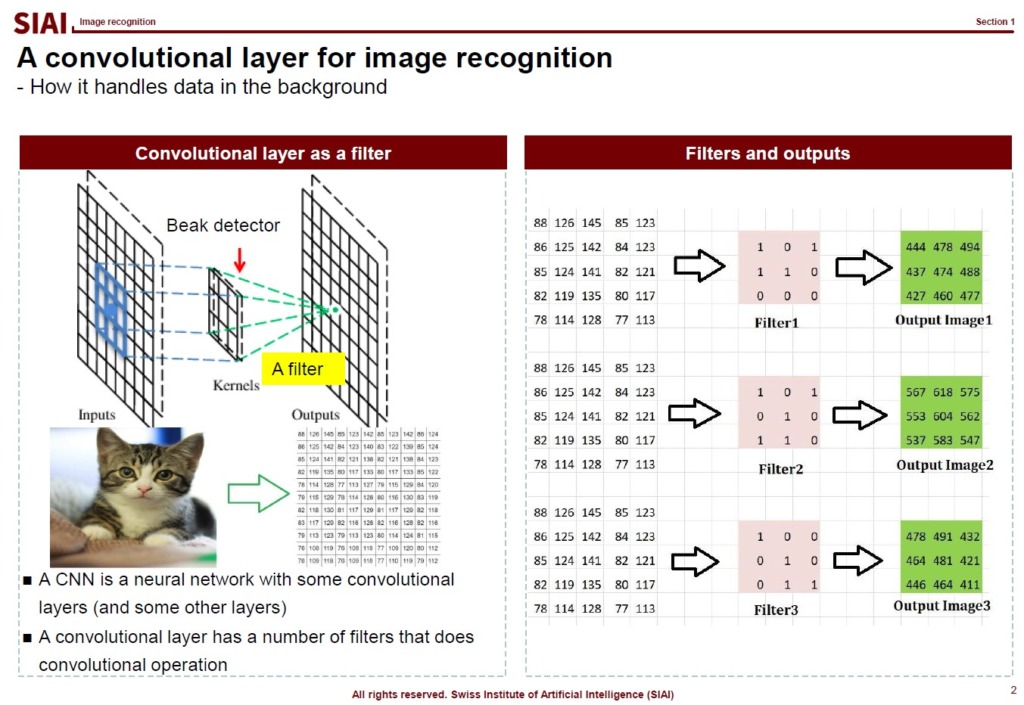
When a modeler tries to feed the image data to the model, it relies on sliding for various reasons. The slider is also known as a filter, which is widely used for photo filtering. SNS images, for example, are frequently modified. The filter you can find in the photo app or an SNS app is basically the same as the slider that we use in image recognition.

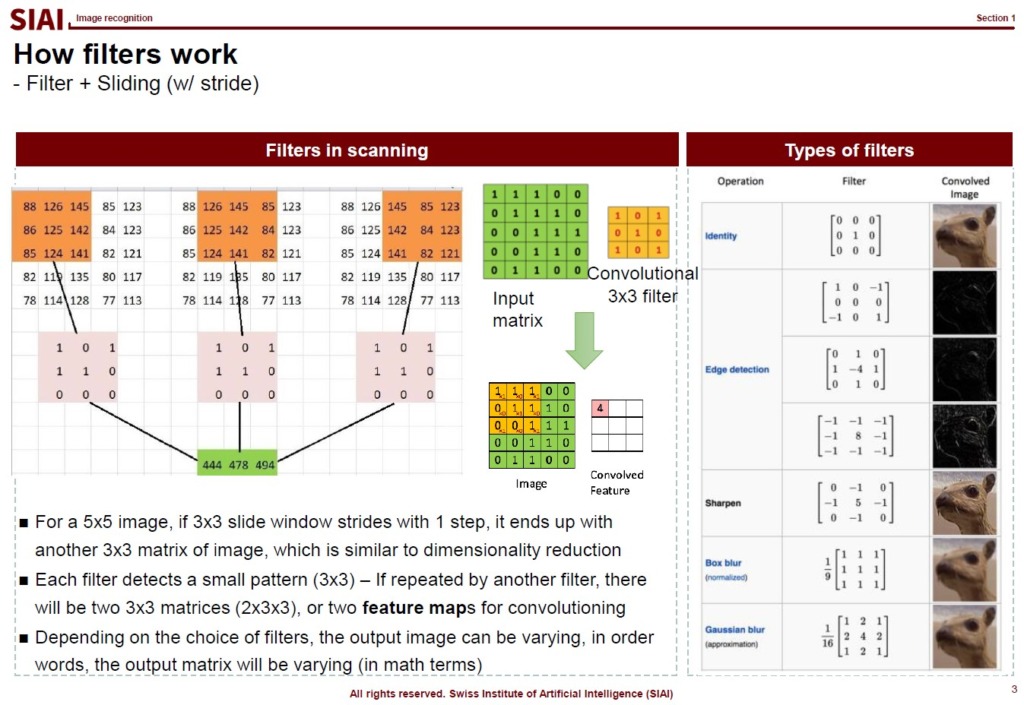
Depending on your choice of the filter, the output matrix becomes different. It may help you to have black/white effect or sharpening. There are thousands of different filters.

One of the key reasons that we rely on the slider in image recognition is, after the sliding, the feed data size becomes smaller. The higher resolution the image is, the more data the Neural Network has to process. Given that Neural Network model is known as one of the the most computational cost consuming method, it is strictly preferred to reduce the image data size. One does not want to lose the important features of the data, just like we use PCA. This is why the choice of filter is a key component of the successful image recognition. For some images, filter A can perform magnificently better than filter B.

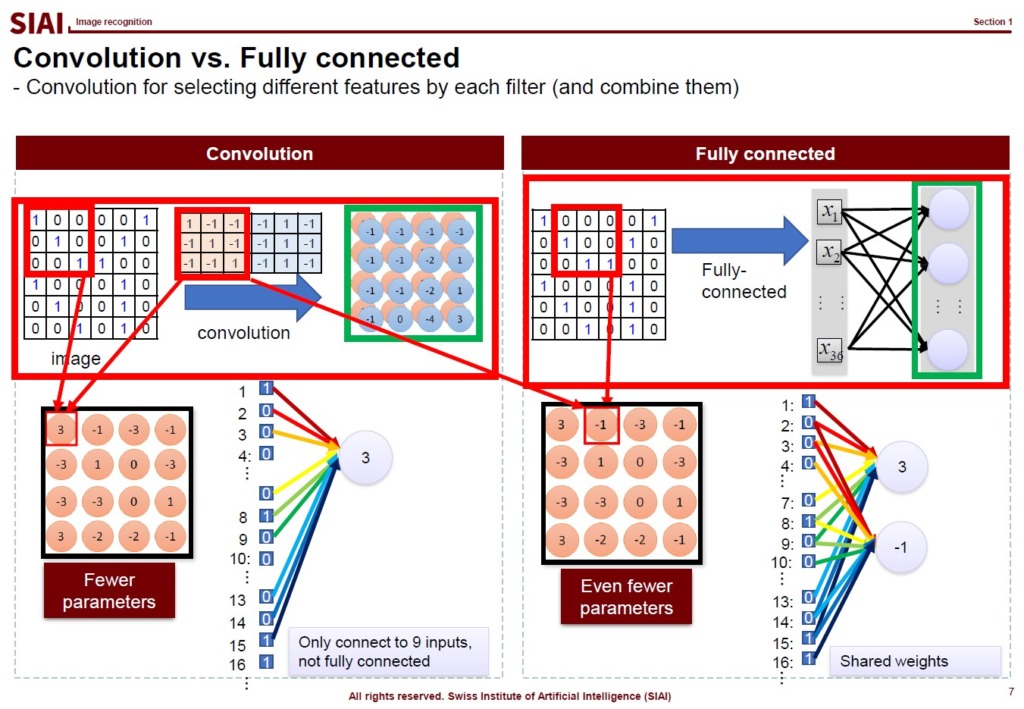
Another technique that we rely on for image recognition is convolutioning. From the slided, or scanned, image data, fully connected neural network forces us to find weights for all links. The convolution helps us to avoid such overlaps, which can further minimize computational costs.

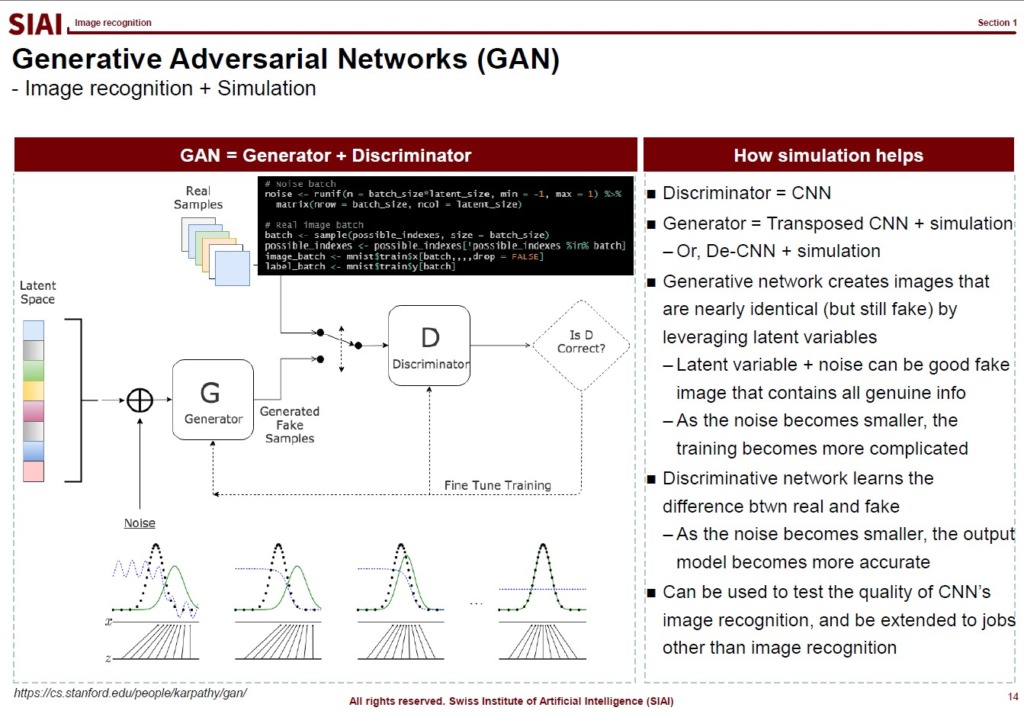
To help you to understand that CNN based image recognition model is still an extension of factor analysis, let's talk little bit of Generative Adversarial Networks (GAN).

The model captures a couple of latent features of the image at the beginning. Just like the first stage of autoencoder, the choise of latent nodes is a key to build a winning model in accuracy and speed. From the latent components, the CNN's convolutioning helps us to further speed up finding weights. The GAN model itself is just another variation of MCMC sampling. You just create a lot of images with some random error from the same latent space. The error imposed images are considered fake images. Your discreminator is supposed to exclude the fakes. It then becomes a simple classification problem. By the artificially created fake image data, the model can learn from more number of data. As discussed in COM501: Scientific Programming, the simulation can help us to find the true population in that $I_M \rightarrow I$ as $M \rightarrow \infty$.

Constructing an Autoencoder model looks like an art, if not computationally heavy work. A lot of non-trained data engineers rely on coding libraries and a graphics card (that supports 'AI' computation), and hoping the computer to find an ideal Neural Network. As discussed in previous section, the process is highly exposed to overfitting, local maxima, and humongous computational cost. There must be more elegant, more reasonable, and more scientific way to do so.

Let's think about a multi-layered neural network model. From the eyes of Factor Analysis, each layer is one round of factor analysis. The factor analysis is in fact a re-contruction of vector space, as was discussed in PCA. In sum, the multi-layered neural network model is a series of re-constructions in vector space. What is the re-construction doing? By PCA, it orthogonalizes data's dimension. Factor analysis in general changes the vector space's key axes. In statistical terms, it is a transformation of density functions from one to another. Both processes preserve the data's hidden information. The vector space as a whole is the same. Only axes are different. Density functions are different, but information in the data set is still the same.

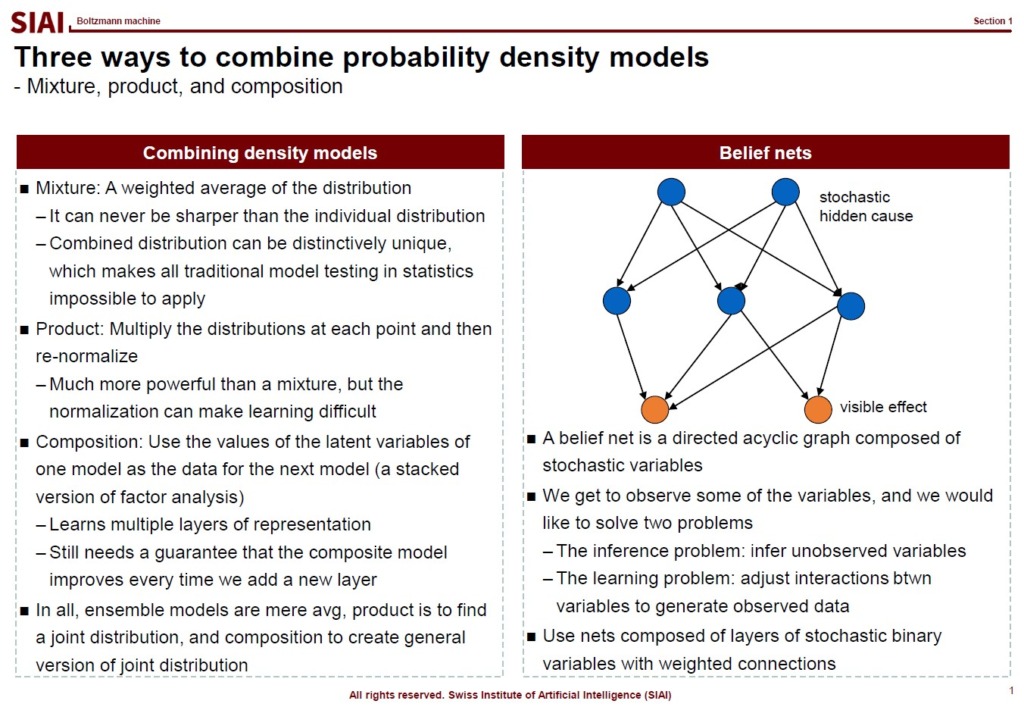
Since each node is a marginal density function and the combination of them on each layer is a joint density, moving from one layer to another layer is a transformation of one joint density to another. In the density, it is no more than a multiplication of functions, if they are independent. However, between two layers, we know that the deep learning structure has dependency to each other. Assuming that the first layer is the data input, then the second layer depends on how much weights are assigned to each link. Depending on the structure of the second layer and weights, the third layer is affected. Once the feed forward process is done, then the back propagation is the opposite process. Though the chain rule helps us to avoid painstaking calculations in each step, nonetheless, the dependency to each layer remains.

This is where we need MCMC, or more specifically Gibbs sampling type approximation. Note that Gibbs sampling assumes input data's distribution, and expects what will be the outcome's density. Once done, then the outcome's density becomes the new input, and we use the information to re-construct the outcome, which is the original input. By running back and forth, the process is expected to converge. Although the correlation between nodes can be a bothersome issue, either over- or under-estimating key weights, such irregularity can be handled by Metropolis-Hastings type corrections. Gibbs class samplings are, in short, two groups of dependent sampling process, instead of a single group. The Bayesian technique precisely fits to our autoencoder problem.

Note that constructing a belief network for rational model has to deal with multiple intrinsic problems. (Mentioned in the aboved screen-captured lecture note). All of them can be successfuly handled by Gibbs type autoencoder.

The structure is known as 'Restricted Boltzmann Machine (RBM)'.

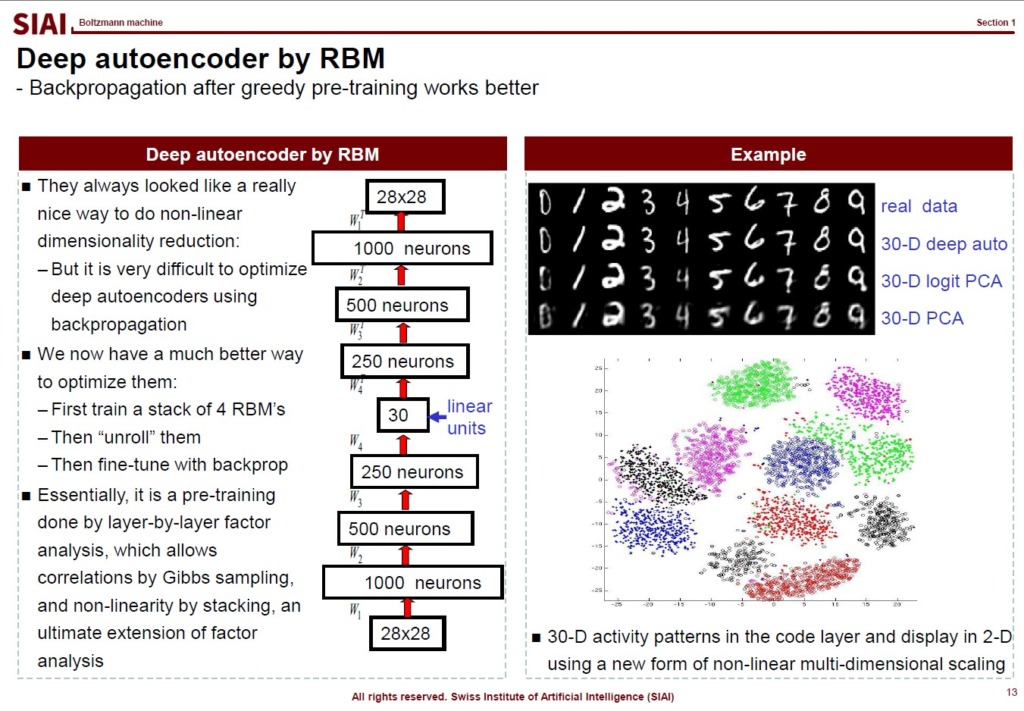
As is illustrated in the above lecture note, the model can capture key hidden factor components better than PCA.

Bayesian estimation tactics can be used to replace arbitrary construction of deep learning model's hidden layer. In one way, it is to replicate Factor Analysis in every layer construction, but now that one layer's value change affects the other layers. This process goes from one layer to all layers. What makes this job more demanding is that we are still unsure the next stage's number of nodes (or hidden factors) are right, precisely as we are unsure about the feeding layer's node numbers. In fact, everything here is unsure, and reliant to each other. This is where Bayesian help us in less arbitrary manner.

Let's think about what we learn from basic Bayesian courses. By a handful of sample data, we assume probable distribution A, B, and C as candidates for the entire population. Say we give 1/3 probability to each. Bayesians call it 'Prior'. We find another sample data, which works like a new weight to distributions. In Bayesian world, we call it 'Likelihood'. Combining the 'Prior' and 'Likelihood', we can find 'Posterior'. With another set of sample data, we can do the process again, as we place the 'Posterior' as the 'Prior'. We do this process Nth times, and at some point, the 'Posterior' hardly is affected by 'Likelihood'. The final 'Posterior' is the probability assignment that we initially looked for. We can do the same process with A, B, C, and D distributions, or even more candidates that fit to sample data.

The structure of Bayesian 'learning' in fact is similar to what we do with Feed Forward and Back Propagation in multiple loops. This is where Bayesian meets Deep Learning.

MCMC (Monte-Carlo + Markov-Chain) simulation

The term MCMC is closely related to Bayesian model building by ways of creating probably simulated data and make the model to learn by itself.

The first MC, Monte Carlo, means a simulation by a prior assumptions on data set's distribution. Recall the basics from COM501: Scientific Programming that by LLN (Law of Large Number), MC approximates $I_M \rightarrow I$ as $M \rightarrow \infty$. In Bayesian, more data helps us to closely approximate the true underlying distribution, when population density is unknown. Remember that we are unsure about the number of nodes in each layer of Autoencoder. So, as long as we can construct a convergence path, the outcome will be most fitted model that represents the data's hidden structure.

The second MC, Markov-Chain, is to explain each simulation's independency to other simulated samples. In other words, we assume i.i.d draws, which ensures unbiased convergence in Monte Carlo process. This helps us if our data follows i.i.d. For example, when we do image recognition, each image's numbers are independent to each other. It is not like I am going to have number 6 in the next flip, if I have number 5 now. And when we feed images to the model, we already preprocess the image by sliding windows, which will be re-visited in image recognition part.

Overall, the MCMC simulation greatly helps us to construct an ideal Autoencoder model without arbitrarily experimenting all possible combinations of data. One may still rely on stepwise type searching, but given the risk of overfitting, local maxima, and exponentially increasing computational cost, it is always wise to rely on more scientific tools like MCMC.

In the lecture, Gibbs sampling, the most well-known MCMC technique, is presented for a sample construction of the Autoencoder. One can also rely on Metropolis-Hastings, if tampering marginal distribution by truncation is necessary.

As was discussed in [COM502] Machine Learning, the introduction to deep learning begins with history of computational methods as early as 1943 where the concept of Neural Network first emerged. From the departure of regression to graph models, major building blocks of neural network, such as perceptron, XOR problem, multi-layering, SVM, and pretraining, are briefly discussed.

As for the intro, logistic regression is re-visited that whatever the values are in the input, the outcome is converted to only a number from 0 to 1. To find the best fit, the binary loss function is introduced in below format.

$\mathcal{L} (\beta_0, \beta_1) = \Sigma_{i} y_i \log{p_i} + (1-y_i) \log{(1-p_i)}$

The function is to minimize losses in both cases where $y=0$ and $y=1$. The limitation of the logistic regression, in fact any regression style functional format, is that without further assumptions in non-linear shape, the estimation ends up with linear form. Even if one introduces non-linear features like $X^2$, it is still limited to functional format. Support Vector Machine (SVM) departs from such limitation, but it still has to be pre-formated.

Neural Network partly solves the limitation in that it allows researchers to by-pass equational assumptions and let the function to find the best fit to the data. Though it still is dependant upon how the form of neural network is structured, what activation functions are used, and how much relevant data is fed to the network, it is a jump start from the functionally limited estimation strategies that had been pre-dominant in computational methods.

In essense, the loss functional shape is the same, but the way deep learning deal with the optimization is to leverage chain rule in partial derivative, therefore speed up the computationally heavy calculation.

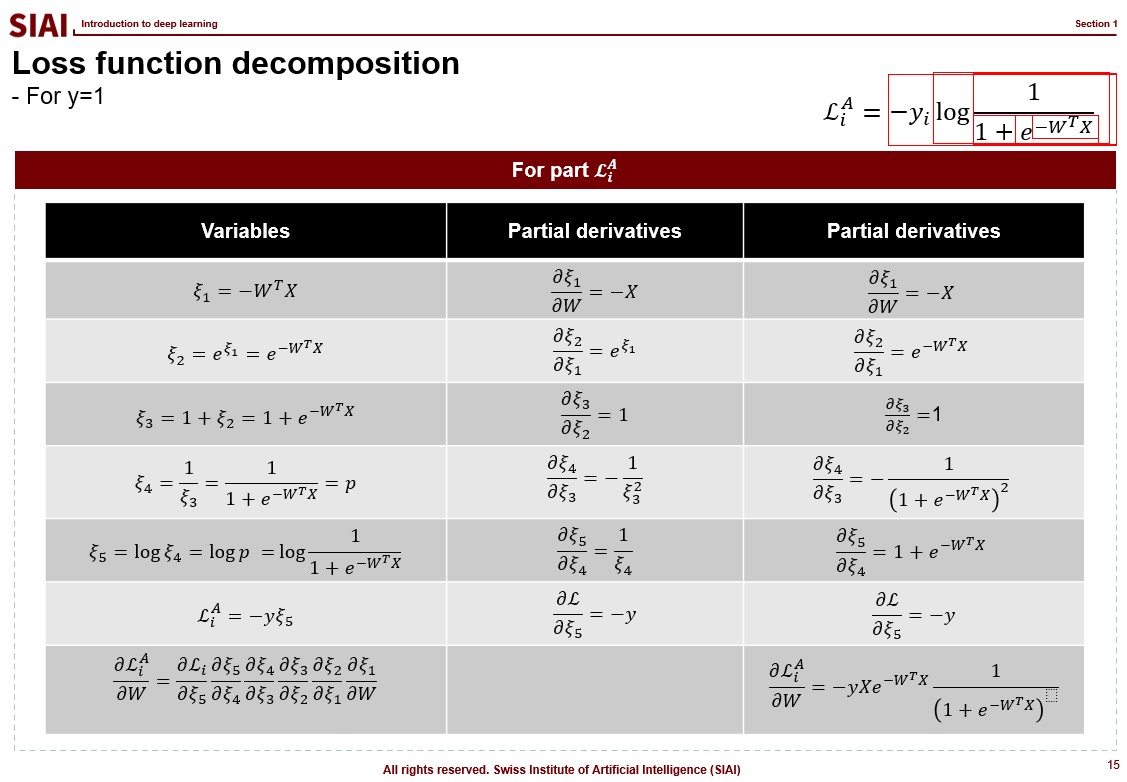
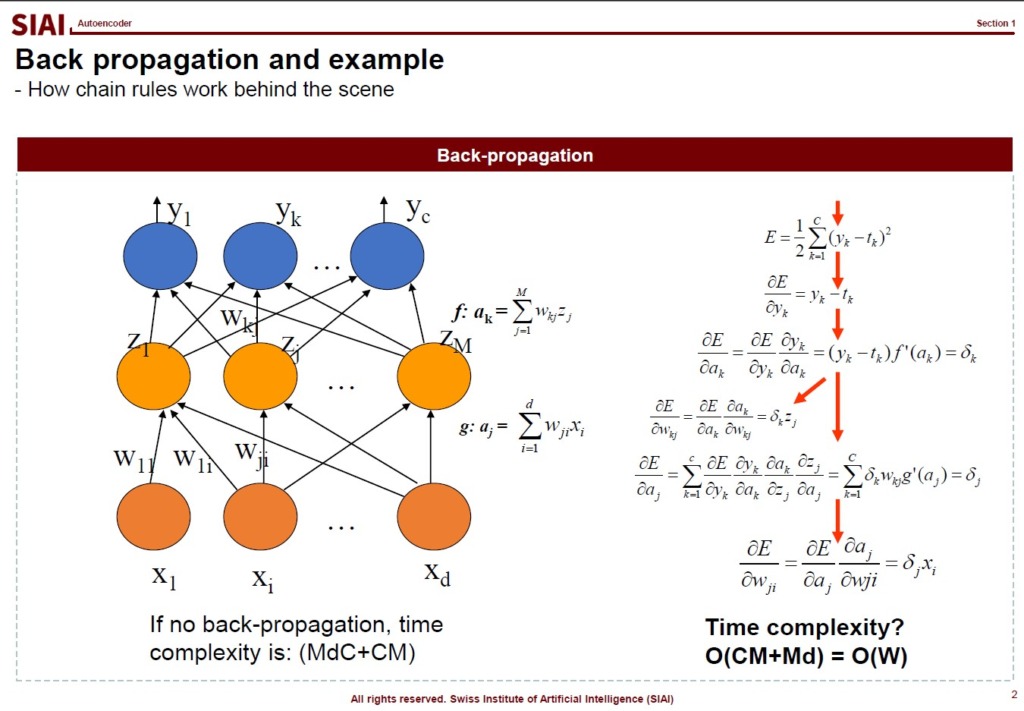
With the benefit of decomposition and chained-partial differentiation, back-propagation can achieve speed of computation that simply needs a single higher order matrix (or tensor) type transaction, instead of feeding nxk columns. An example of such is illustrated below.

To further speed up the computation, one can modify the gradient approximation with varying weights, disproportional learning rates for vertical/horizontal angles, or even with correction by dynamically changing second moment (or variance-covariance) structure. In fact, any optimization is possible, depending on the data structure. In general, Adam optimizer performs marginally faster than RMSProp as it incorporates both first and second moments. The advantage will most likely disappear if the fed data set does not have dynamically changing variance for the reasons that second moment does not have any more information than base case.

Feed forward and back propagation have significant advantage in terms of speed of calculation and error correction, but it does not mean that we can eliminate the errors. In fact the error enlarges if the fed data leads the model to out of convergence path. The more layers there are, the more computational resources required, and the more prone to error mis-correction due to the structure of serial correction stages in every layer.

The reason we rely on Neural Network model is because we need to find a nested non-linear structure of the data set, which cannot be done by other computational models, such as SVM. Then, is there a way to fix the mis-correction? Partly, it can be done by drop-outs, but one has to compromise loss of information and the structure of drop-out is also arbitrary.

What, instead, can be done is to build an autoencoder model in a way to replicate Factor Analysis in network form. Recall from Machine Learning that Factor Analysis is a general form of Principle Component Analysis (PCA). Though PCA is only limited to linear combination of variables to re-construct the data's vector spaces by variance-covariance matrix. Given that all computational models are in a way to re-structure original data sets to our desired form, PCA could help us to find hidden key components of variance's dimension. i.e. the target of all regression based models, including Neural Network, is to maximize explanatory power in terms of variability matching.

From the vector space of second moments, the combination of explanatory variables does not necessarily have to be linear. This is why we moved away from linear regression and have been exploring all non-linear models. The same works for hidden factors. The combination of variables to match hidden factors does not, again, have to be linear. In Factor Analysis, we have explored a bit that depending on the data's underlying distribution, factor combination can be non-linear.

Here comes the benefit of Autoencoder. We can construct Neural Network model with the concept of Factor Analysis. With the right number of hidden factors, the re-designed Neural Network model not only becomes more robust to changes in data sets, but it also becomes less prone to error mis-correction and/or over-fitting. If one have more than needed hidden factors, it is likely the model is going to be overfit. To deal with it, most frequent choice is drop-out, but the result, as mentioned earlier, is not robust, and sometimes it is no more than an improvision for that specific learning event. To small number of hidden factors in a particular layer obviously results in insufficient learning.

To help you to follow Autoencoder's logic in network building, let's talk about matching number 0 to 9 in shapes in image recognition. By PCA, as discussed in Machine Learning, one tries to find PCs from transformed image. Some PCs may help us to differenciate 0 and 3, but that particular PC is not the strongest vector space that we usualy look for in PCA based regressions (PCR). Together with other similar images like 9, the upper right parts of the images will give us one PC due to commonality. Here in image recognition, we need PCs from common parts for some guessing, at the same time we also need uncommon parts' PC to differentiate 0, 3, and 9. There could be over 100 PCs initially, but eventually, we need 10 hidden factors to verify 0 to 9.

The same thought experiment can be constructed by a rather a huge size of Neural Network. Your end layer will have 10 nodes, but at the beginning, you may need over 100 nodes, just like PCA. The construction of multiple hidden layers in the middle, coined as 'Encoder', should be carefully designed to pick up separable PCs at first, then exclude unnecessary PCs for the end goal. Like we have witnessed in tree-based models, creating a non-linear function requires a number of different layers.

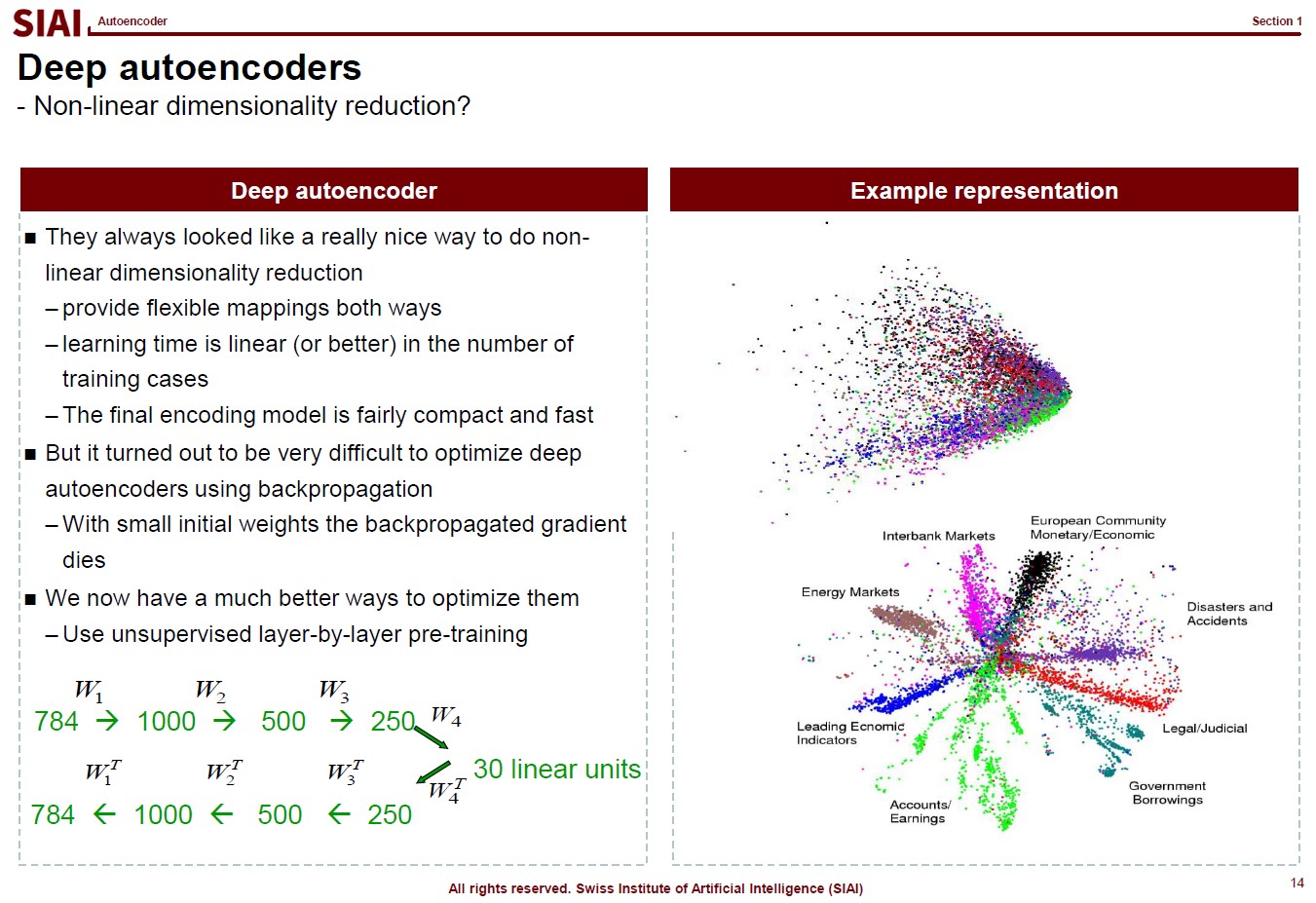
If the 'Encoder' is designed well, for any data that fits to your data-preprocessing for image 0 to 9, it should not be that difficult to unwind the process and recover the original data (or very close to original data). In short, it is a network version of Factor Analysis that combines 'from' and 'to'.

This process is called Autoencoder, which can be used to not only for image recognifition, but it can also be used to non-linear simulation like GAN (Generative Adversarial Network).

To further optimize the painstaking encoder construction, we can borrow Bayesian estimation tactics.