[해외DS]는 해외 유수의 데이터 사이언스 전문지들에서 전하는 업계 전문가들의 의견을 담았습니다. 저희 데이터 사이언스 경영 연구소 (MDSA R&D)에서 영어 원문 공개 조건으로 콘텐츠 제휴가 진행 중입니다.

---

뫼비우스의 띠는 흥미로운 수학적 대상이다. 안과 밖의 구별이 없는 이 단면 표면을 만들려면 종이 조각을 가져다가 한 번 비틀고 끝을 테이프로 붙이면 된다. 어린아이들도 할 수 있을 정도로 간단하게 뫼비우스 띠를 만들 수 있지만, 도형의 성질은 수학자들의 지속적인 관심을 끌 만큼 복잡하다.

뫼비우스의 띠를 만들 수 있는 최소 길이는?

1858년 뫼비우스 띠를 발견한 공로로 두 명의 독일 수학자 아우구스트 페르디난트 뫼비우스(August Ferdinand Möbius)와 요한 베네딕트 리스팅(Johann Benedict Listing)를 언급하지만 수학의 거장 칼 프리드리히 가우스(Carl Friedrich Gauss)도 같은 시기에 이 도형을 알고 있었다는 증거가 있다고 스토니브룩 대학교의 수학자인 모이라 차스(Moira Chas)가 말했다. 뫼비우스 띠에 대해 누가 처음 생각했는지에 관계없이, 최근까지 연구자들은 겉보기에 쉬운 질문 하나에 당황했다: "뫼비우스 띠를 만드는 데 필요한 가장 짧은 종이 길이는 무엇일까?" 브라운 대학교의 수학자 리처드 에반 슈워츠(Richard Evan Schwartz)는 Embedded 형태, 즉 스스로 관통하거나 교차하지 않는 매끄러운 뫼비우스 띠의 경우 이 문제가 해결되지 않았었다고 설명했다. Immersed 형태는 종이 길이가 짧아도 겹진 상태로 뫼비우스의 띠를 만들 수 있지만, Embedded 띠는 종이가 서로 겹치는 것을 허용하지 않기 때문에 종이 길이가 너무 짧으면 뫼비우스의 띠를 만들 수 없게 된다. 바로 이지점이 Embedded 띠가 가질 수 있는 최소 길이에 대한 궁금증을 갖게 되는 동기다.

1977년 수학자 찰스 시드니 위버(Charles Sidney Weaver)와 벤자민 리글러 할펀(Benjamin Rigler Halpern)은 최소 길이에 대한 이 질문을 제기하면서 "뫼비우스 띠가 자기 교차점을 갖도록 허용하면 문제가 쉬워진다"고 말했다고 캘리포니아 대학교 데이비스 캠퍼스의 수학자 드미트리 푹스(Dmitry Fuchs)가 전했다. 남은 질문은 "비공식적으로 말하자면 자기 교차점을 피하고자 얼마나 많은 공간이 필요한지 결정하는 것"이라고 푹스는 덧붙였다. 할펀과 위버는 최소 크기를 가정했지만, 할펀-위버 추측이라고 불리는 이 아이디어를 증명할 수는 없었다.

남다른 슈워츠의 증명 방식

슈워츠는 약 4년 전 펜실베이니아 주립대의 수학자 세르게이 타바치니코프(Sergei Tabachnikov)를 통해 이 문제를 처음 알게 됐고, 타바치니코프와 푹스가 쓴 책에서 이 주제에 관한 챕터을 읽었다. "그 챕터를 읽고 완전히 매료되었습니다"라고 그는 회상했다. 그의 왕성한 호기심은 문제에 대한 해결책으로 결실을 보았다. 슈워츠는 8월 24일 arXiv.org에 게재된 논문에서 할펜-위버의 가설을 증명했다. 그는 종이로 만든 Embedded 형 뫼비우스 띠는 가로세로비가 √3(약 1.73)보다 큰 경우에만 구성할 수 있음을 보여주었다. 예를 들어 띠의 너비가 1cm인 경우 길이는 √3cm보다 길어야 한다.

이 난제를 해결하려면 창의력이 필요했다. 일반적인 접근 방식을 사용하면 "공식을 사용하여 자기 교차하는 표면과 자기 교차하지 않는 표면을 구별하기가 항상 어렵습니다"라고 푹스가 강조했다. "이 어려움을 극복하려면 슈워츠의 기하학적 시각이 필요합니다. 하지만 이런 시도는 매우 드뭅니다!"

독일 괴팅겐 대학의 수학자인 맥스 와데츠키(Max Wardetzky)는 "슈워츠는 큰 문제를 작은 조각들로 분해했으며, 각 조각은 기본적인 기하학만 있으면 풀 수 있는 쉬운 문제로 변했습니다"라고 감탄했다. "이러한 증명 방식은 가장 순수한 형태의 우아함과 아름다움을 구현해 냅니다."

그러나 슈워츠는 증명에 성공하기 전까지 몇 년에 걸쳐 다른 전략을 시도했다가 실패했었다. 그러다 최근 그는 2021년 논문에서 사용했던 접근 방식이 효과가 있었어야 한다는 생각이 들어 이 문제를 다시 검토하기로 했다. 그의 직감이 맞았다. 문제 조사를 재개했을 때 그는 이전 논문에서 'T-패턴'과 관련된 중간 결과인 한 부명제(lemma)에 실수가 있음을 발견했다. 슈워츠는 이 오류를 수정함으로써 할펀-위버의 가설을 빠르고 쉽게 증명했다. 그 실수만 아니었다면 3년 전에 이 문제를 해결했을 것이라고 슈워츠는 말했다.

"평행사변형이 아니었어?"

할펀-위버 추측에 대한 슈워츠의 해결책에서 T-패턴 부명제는 굉장히 중요한 구성 요소였다. "뫼비우스 띠는 '선직면'(ruled surface)이라고 불리는 직선들이 있습니다"라고 그는 설명하기 시작했다. 다른 종이 물체도 이 속성을 공유하고, "한 공간에 종이가 있을 때 그것이 복잡한 위치에 있더라도 모든 지점에는 직선이 통과합니다."라고 슈워츠는 말했다. 이 직선이 뫼비우스 띠를 가로질러 양쪽 끝에서 경계에 부딪히도록 그리는 것을 상상할 수 있다.

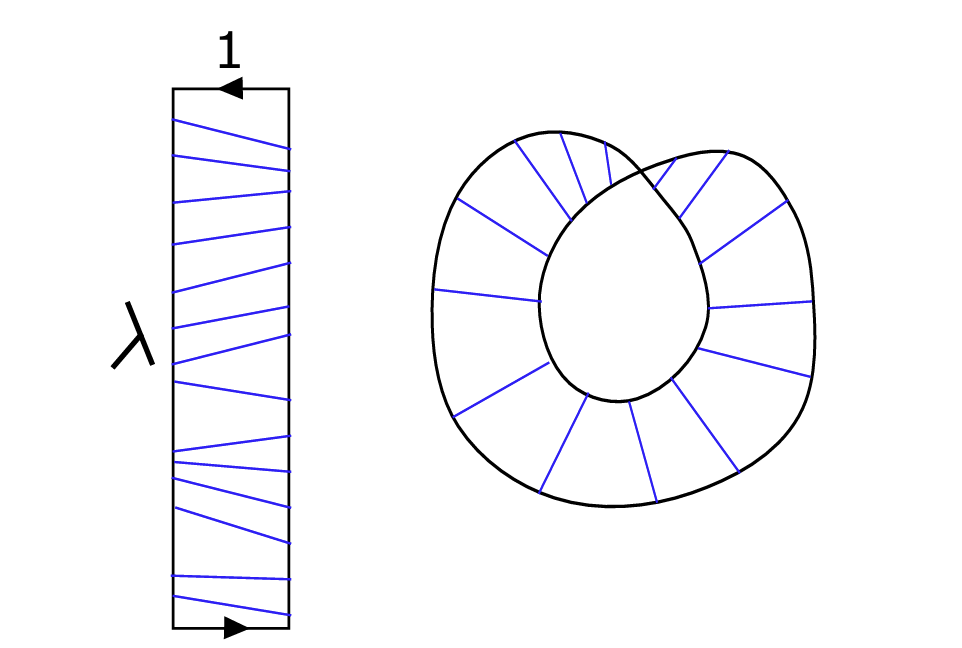
슈워츠는 이전 연구에서 서로 수직이면서 같은 평면에 있는 두 개의 직선이 모든 뫼비우스 띠에 T 패턴을 형성하는 것을 확인했다. 아래 그림에서 진한 파란색 선이 있는 뫼비우스의 띠가 지구본처럼 오른쪽으로 회전하고 있다고 상상해 보자. 진한 파란색 선이 반대편에 도달했을 때는 뫼비우스의 성질로 인해 파란색 점선처럼 뒤집혀 있을 것이다. 두 직선을 겹쳐서 본다면 수직을 이루는 걸 확인할 수 있다. 이 한 쌍의 직선을 T 패턴이라고 부르고 다른 임의의 직선에 대해서도 동일한 T 패턴을 발견할 수 있다. T 패턴의 존재가 수수께끼를 푸는 첫 번째 단추였다.

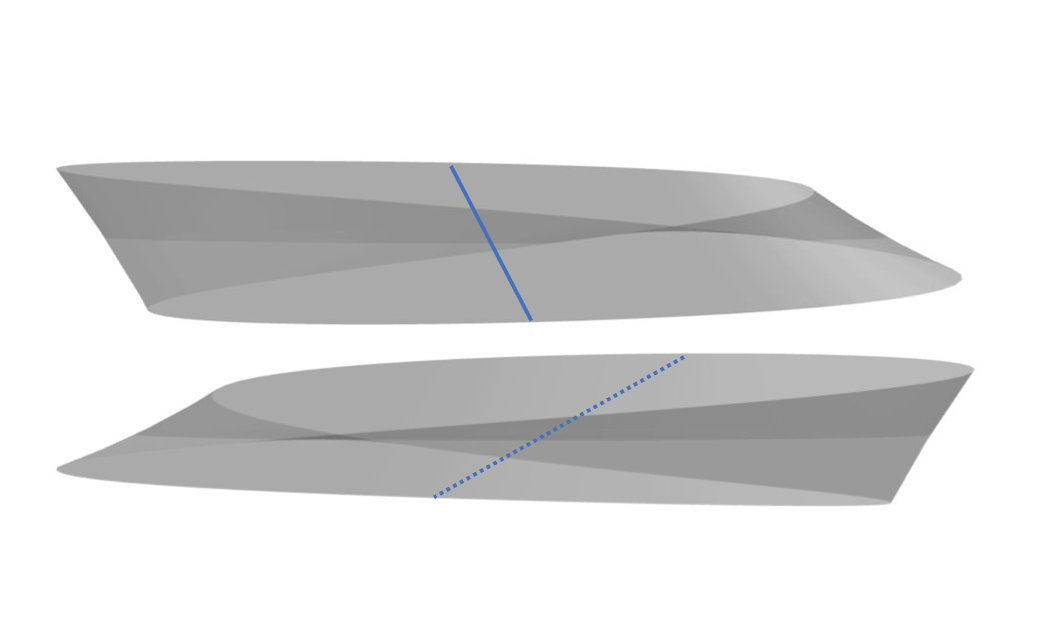
다음 단계는 뫼비우스 띠를 파란색 선을 따라 비스듬한 방향으로 잘라내고 잘린 모양을 고려해서 최소 길이를 찾아내는 최적화 작업이다. 이 단계에서 슈워츠는 2021년 논문에서 잘린 도형이 평행사변형이라고 잘못 결론을 내려 틀린 결괏값을 얻었다.

올여름, 슈워츠는 다른 방법을 시도하기로 하고 종이 뫼비우스 띠를 납작하게 평면화해서 실험하기 시작했다. 그는 "뫼비우스 띠를 평면으로 누를 수 있다는 것을 보여줄 수 있다면 평면 물체만 생각하면 되는 더 쉬운 문제로 단순화할 수 있을 것"이라고 생각했다.

실험 도중 뫼비우스 띠를 자르던 슈워츠는 깜짝 놀랐다. "맙소사, 이건 평행사변형이 아니구나! 사다리꼴이었네." 실수를 발견한 슈워츠는 처음에는 화가 났지만("저는 실수하는 것이 싫어요."), 사다리꼴 모형에 맞게 길이를 다시 계산했다. "수정된 계산을 통해 추측했던 숫자가 나왔습니다"라고 그는 전했다. "깜짝 놀랐죠.... 3일 동안 거의 잠을 자지 않고 이걸 작성하는 데만 시간을 보냈습니다"라고 당시 격양된 상황을 설명했다.

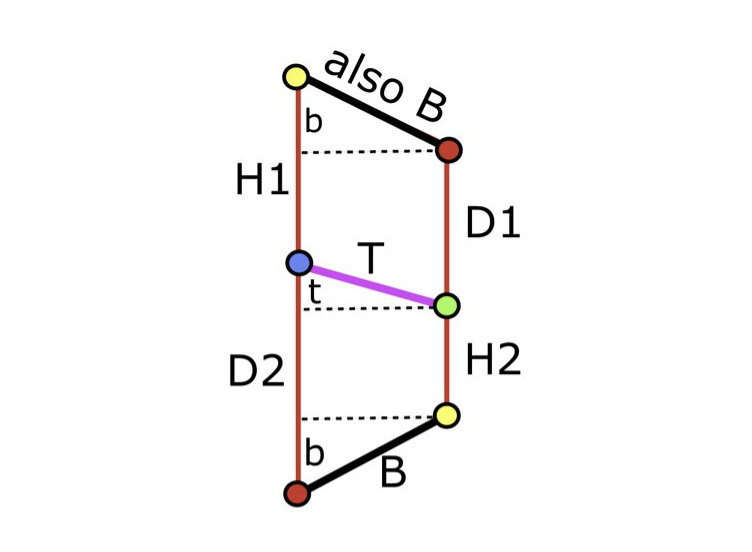
위의 그림에서 같은 색상의 노드끼리 맞춰서(빨강-빨강, 노랑-노랑) 잘린 파란색 선(B)을 꼬아서 다시 붙이면 파란색 선이 분홍색 T 선과 수직임을 눈으로 다시 한번 확인 할 수 있고, 아래와 똑같은 평면상의 종이접기 문제로 단순화할 수 있음을 직관적으로 느낄 수 있을 것이다.

실습하면서 T 패턴을 발견한 슈워츠의 기쁨을 함께 누려보자. 뫼비우스의 띠를 하나 만들어서 비스듬한 파란색 직선을 먼저 그린다. 띠를 반대편으로 돌리면서 뒤집히는 모양도 확인해 보고 원래 위치의 선과 수직을 이루는 것도 상상한다(원래 위치의 직선 모양을 기억하고 있어야 한다). 그 후 선을 따라 자르면 사다리꼴이 나온다. 잘린 선들을 원래 위치로 다시 붙이는 과정에서 반대편에 뒤집힌 선과의 수직을 이루는 것을 더 확실하게 볼 수 있다. 아래 색종이 접기도 직접 해보면 위와 똑같은 행위임을 느낄 수 있다. 결국 뫼비우스의 띠에서 모든 임의의 파란색 선(비스듬한 직선)에 대해 똑같이 T 패턴을 찾을 수 있기 때문에 아래의 간단한 종이 접기 문제로 간소화할 수 있다. 슈워츠의 비범함이 여기서 나타난다.

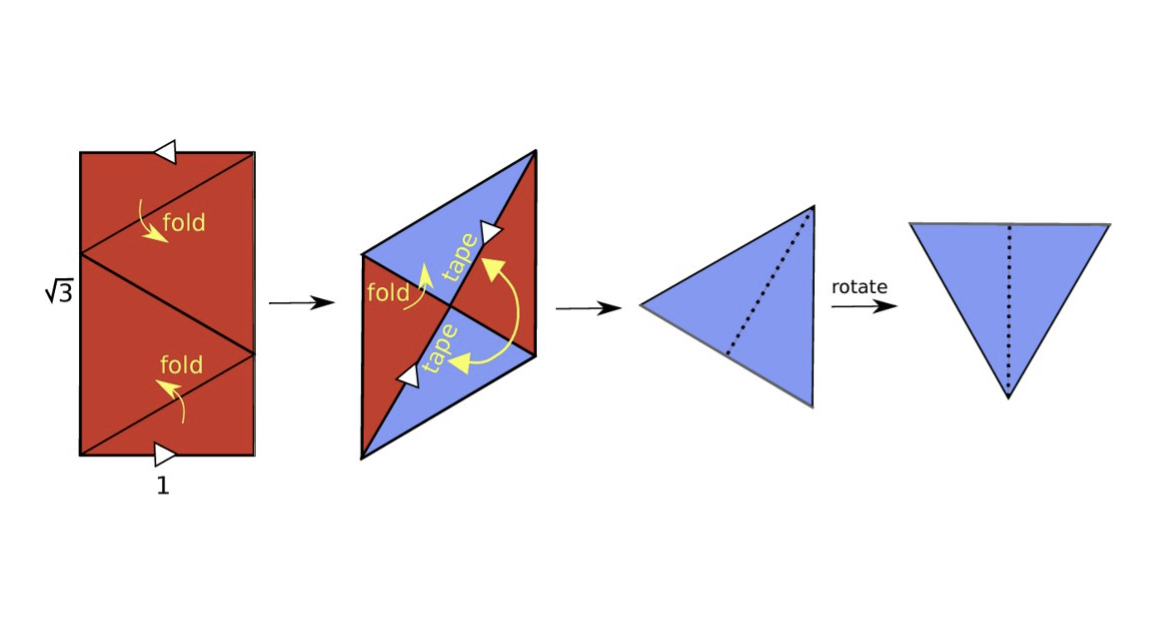
마침내 반세기가 넘은 질문에 대한 답이 나왔다. 타바치니코프는 "오랫동안 풀리지 않았던 문제를 해결하려면 용기가 필요하다"라고 말했다. "이것은 리처드 슈워츠의 수학에 대한 접근 방식의 특징입니다. 그는 쉬워 보이지만 어렵다고 알려진 문제를 공격하는 것을 좋아합니다. 그리고 그는 이전 연구자들이 미처 발견하지 못한 새로운 측면을 발견합니다."

"저는 수학을 인류의 공동 작업이라고 생각합니다"라고 차스는 운을 뗐다. "뫼비우스, 리스팅, 가우스에게 '당신이 시작했고, 이제 이것 좀 보세요...'라고 말할 수 있으면 좋겠어요. 아마도 수학의 하늘 어딘가에서 그들은 우리를 바라보며 '오, 이런!'이라고 생각할 것입니다."

수학자들은 뫼비우스 띠를 얼마나 길게 만들 수 있는지에 대한 제한이 없다는 것을 이미 알고 있다(물리적으로 뫼비우스 띠를 만드는 것은 언젠가는 번거로워지겠지만 말이다). 하지만 한 장이 아닌 세 장이 꼬인 뫼비우스 띠를 만드는 데 사용할 때 종이의 길이가 얼마나 짧을 수 있는지는 아무도 모른다고 슈워츠는 지적합니다. 더 일반적으로는 "홀수 개의 꼬임을 만드는 뫼비우스 띠의 최적 크기에 관해 물어볼 수 있습니다."라고 타바치니코프는 말했다. "가까운 시일 내에 누군가가 이 문제를 해결할 것으로 기대합니다."

---

Möbius strips are curious mathematical objects. To construct one of these single-sided surfaces, take a strip of paper, twist it once and then tape the ends together. Making one of these beauties is so simple that even young children can do it, yet the shapes’ properties are complex enough to capture mathematicians’ enduring interest.

The 1858 discovery of Möbius bands is credited to two German mathematicians—August Ferdinand Möbius and Johann Benedict Listing—though evidence suggests that mathematical giant Carl Friedrich Gauss was also aware of the shapes at this time, says Moira Chas, a mathematician at Stony Brook University. Regardless of who first thought about them, until recently, researchers were stumped by one seemingly easy question about Möbius bands: What is the shortest strip of paper needed to make one? Specifically, this problem was unsolved for smooth Möbius strips that are “embedded” instead of “immersed,” meaning they “don't interpenetrate themselves,” or self-intersect, says Richard Evan Schwartz, a mathematician at Brown University. Imagine that “the Möbius strip was actually a hologram, a kind of ghostly graphical projection into three-dimensional space,” Schwartz says. For an immersed Möbius band, “several sheets of the thing could overlap with each other, sort of like a ghost walking through a wall,” but for an embedded band, “there are no overlaps like this.”

In 1977 mathematicians Charles Sidney Weaver and Benjamin Rigler Halpern posed this question about the minimum size and noted that “their problem becomes easy if you allow the Möbius band you are making to have self-intersections,” says Dmitry Fuchs, a mathematician at the University of California, Davis. The remaining question, he adds, “was to determine, informally speaking, how much room you need to avoid self-intersections.” Halpern and Weaver proposed a minimum size, but they couldn’t prove this idea, called the Halpern-Weaver conjecture.

Schwartz first learned about the problem about four years ago, when Sergei Tabachnikov, a mathematician at Pennsylvania State University, mentioned it to him, and Schwartz read a chapter on the subject in a book Tabachnikov and Fuchs had written. “I read the chapter, and I was hooked,” he says. Now his interest has paid off with a solution to the problem at last. In a preprint paper posted on arXiv.org on August 24, Schwartz proved the Halpern-Weaver conjecture. He showed that embedded Möbius strips made out of paper can only be constructed with an aspect ratio greater than √3, which is about 1.73. For instance, if the strip is one centimeter wide, it must be longer than √3 cm.

Solving the quandary required mathematical creativity. When one uses a standard approach to this type of problem, “it is always difficult to distinguish, by means of formulas, between self-intersecting and non-self-intersecting surfaces,” Fuchs says. “To overcome this difficulty, you need to have [Schwartz’s] geometric vision. But it is so rare!”

In Schwartz’s proof, “Rich managed to dissect the problem into manageable pieces, each of which essentially necessitated only basic geometry to be solved,” says Max Wardetzky, a mathematician at the University of Göttingen in Germany. “This approach to proofs embodies one of the purest forms of elegance and beauty.”

Before arriving at the successful strategy, however, Schwartz tried other tactics on and off again over a few years. He recently decided to revisit the problem because of a nagging sensation that the approach he had used in a 2021 paper should have worked.

In a way, his gut feeling was correct. When he resumed investigating the problem, he noticed a mistake in a “lemma”—an intermediate result—involving a “T-pattern” in his previous paper. By correcting the error, Schwartz quickly and easily proved the Halpern-Weaver conjecture. If not for that mistake, “I would have solved this thing three years ago!” Schwartz says.

In Schwartz’s solution to the Halpern-Weaver conjecture, the T-pattern lemma is a critical component. The lemma begins with one basic idea: “Möbius bands, they have these straight lines on them. They’re [what are] called ‘ruled surfaces,’” he says. (Other paper objects share this property. “Whenever you have paper in space, even if it’s in some complicated position, still, at every point, there’s a straight line through it,” Schwartz notes.) You can imagine drawing these straight lines so that they cut across the Möbius band and hit the boundary at either end.

In his earlier work, Schwartz identified two straight lines that are perpendicular to each other and also in the same plane, forming a T-pattern on every Möbius strip. “It is not at all obvious that these things exist,” Schwartz says. Showing that they do was the first part of proving the lemma, however.

The next step was to set up and solve an optimization problem that entailed slicing open a Möbius band at an angle (rather than perpendicular to the boundary) along a line segment that stretched across the width of the band and considering the resulting shape. For this step, in Schwartz’s 2021 paper, he incorrectly concluded that this shape was a parallelogram. It’s actually a trapezoid.

This summer, Schwartz decided to try a different tactic. He started experimenting with squishing paper Möbius bands flat. He thought, “Maybe if I can show that you can press them into the plane, I can simplify it to an easier problem where you’re just thinking of planar objects.”

During those experiments, Schwartz cut open a Möbius band and realized, “Oh, my God, it’s not the parallelogram. It’s a trapezoid.” Discovering his mistake, Schwartz was first annoyed (“I hate making mistakes,” he says) but then driven to use the new information to rerun other calculations. “The corrected calculation gave me the number that was the conjecture,” he says. “I was gobsmacked.... I spent, like, the next three days hardly sleeping, just writing this thing up.”

Finally, the 50-year-old question was answered. “It takes courage to try to solve a problem that remained open for a long time,” Tabachnikov says. “It is characteristic of Richard Schwartz’s approach to mathematics: He likes attacking problems that are relatively easy to state and that are known to be hard. And typically he sees new aspects of these problems that the previous researchers didn’t notice.”

“I see math as a joint work of humanity,” Chas says. “I wish we could tell Möbius, Listing and Gauss, ‘You started, and now look at this....’ Maybe in some mathematical sky, they are there, looking at us and thinking, ‘Oh, gosh!’”

As for related questions, mathematicians already know that there isn’t a limit on how long embedded Möbius strips can be (although physically constructing them would become cumbersome at some point). No one, however, knows how short a strip of paper can be if it’s going to be used to make a Möbius band with three twists in it instead of one, Schwartz notes. More generally, “one can ask about the optimal sizes of Möbius bands that make an odd number of twists,” Tabachnikov says. “I expect someone to solve this more general problem in the near future.”