무한 원숭이 정리에 따르면 원숭이가 셰익스피어 작품을 만들어낼 수 있어
다만 인간이 인지하지 못할 정도로 오랜 시간 기다려야
한 문장을 만들어내는 데만 우주가 한 번 더 태어나고도 남아

[해외DS]는 해외 유수의 데이터 사이언스 전문지들에서 전하는 업계 전문가들의 의견을 담았습니다. 저희 글로벌AI협회 연구소(GIAI R&D)에서 콘텐츠 제휴가 진행 중입니다.

무한 원숭이 정리에 따르면 원숭이가 무한대의 시간을 갖고 무작위로 키보드를 누르다 보면 셰익스피어 작품을 만들 수 있다. 이는 ‘무한’이라는 개념이 인간의 상상을 초월한 크기라는 것을 보여주는 좋은 예시다. 예를 들어 원숭이가 한 문장을 만들어내는 데만 빅뱅부터 현재까지의 시간을 훨씬 뛰어넘지만, 무한의 세계에서는 원숭이가 셰익스피어의 작품을 만들어낼 수 있다.

원숭이가 셰익스피어 작품을 만들어낼 수 있다?

2002년 수학 역사상 가장 재밌는 실험이 진행됐다. 실험은 ‘무한 원숭이 정리’를 증명하는 것을 목표로 설계됐다. 이 정리는 무한한 시간을 가진 원숭이가 키보드를 무작위로 두드리다 보면 셰익스피어 전집을 포함해 모든 문자를 만들어낼 수 있다는 정리다. 실험은 2002년 5월 1일에 시작해 약 7주간 진행됐으며 6마리 원숭이들이 키보드 자판을 두드려 무작위로 글자를 생성하도록 했다.

예상과 달리 원숭이들은 7주 이상 키보드를 두드렸음에도 불구하고 5페이지 분량 밖에 못 만든 데다가 문서는 대부분 'S'로 가득차 있었다. 실험에 참여한 6마리 원숭이를 변호하자면 이들에게는 무한한 시간이 주어져 있지 않았다. 이를 감안하더라도 결과는 예상과 괴리가 너무 커 대중들은 원숭이가 '햄릿'이나 스코틀랜드 연극을 만들어낼 수 있을 지에 대해 회의적인 반응을 보였다.

실험으로 무한 원숭이 정리를 증명하는데 실패했지만, 원숭이가 무작위 글자를 생성하는 데 이상적인 후보가 아니라는 것은 똑똑히 보여줬다. 무한 원숭이 정리는 1913년 수학자 에밀 보렐이 자신의 확률 이론을 설명하기 위해 동물을 은유적으로 사용한 데서 유래됐다. 하지만 이 정리의 배경이 되는 아이디어는 훨씬 더 오래됐다. 고대 로마 철학자이자 정치가인 마르쿠스 툴리우스 키케로는 “1~20개의 활자를 땅에 여러 번 던지다 보면 읽을 수 있는 순서로 떨어질까“라는 문제에, 운으로는 한 구절도 만들 수 없다고 답했다.

그러나 오늘날 연구에 따르면 수학적으로 키케로가 틀렸다는 것이 밝혀졌다. 다시 말해 아주 오랜 시간 기다릴 수 있다면 무작위로 희곡이 나올 수 있다는 말이다.

수학적으로 원숭이가 셰익스피어 작품 만들 수 있어

예를 들어 무작위로 키보드에서 문자를 누를 때 'Banana'라는 단어가 우연히 나올 확률은 얼마일까? 숫자나 특수 문자를 누르지 않는다는 가정 하에 무작위로 선택한 6개의 문자를 연속으로 누를 확률은 약 50억분의 1로 매우 희박하다. 반대로 Banana를 입력하지 않을 확률은 1에서 50억분의 1을 뺀 값으로 1에 가깝다. 6개의 문자를 무작위로 누르면 Banana라는 단어가 나올 가능성이 매우 낮으나, 문자를 더 많이 누를 수 있다면 상황은 달라진다.

7개의 문자를 무작위로 누르면 6글자로 이루어진 두 부분이 있다. 8번 문자를 누르면 6글자로 이루어진 세 개의 문자열이 있다. 이를 일반화하면 키보드를 무작위로 n번 누르면 문자열에 Banana가 없을 확률은 아래의 식과 같다. 따라서 n이 증가할수록 Banana가 문자열 내에 없을 확률은 점차 감소한다.

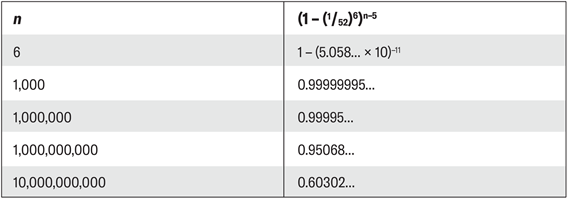
Banana가 문장 내에 존재할 확률은 키보드를 누른 횟수에 비례하다가 100억번 누르면 약 40%까지 증가한다. 키보드를 무수히 많이 누르면 원하는 단어가 포함될 확률은 1에 가까워진다. 따라서 수학적 관점에서 볼 때 키케로의 주장은 틀렸다.

하지만 현실적으로 원숭이가 셰익스피어 작품 만드는 건 불가능해

2024년 브라질 상파울로 대학의 데이터 분석가인 에르곤 쿠글러 데 모라에스 실바는 무작위로 문자를 생성시킬 경우, 셰익스피어의 작품을 만들어내는 데 얼마나 걸릴지 연구했다. 여기서 실바는 ‘S’를 많이 누른 원숭이 대신 문자 생성기를 만들어 실험을 진행했다. 문자 생성기는 햄릿의 유명한 문장인 “To be, or not to be, that is the Question”이 나타날 때까지 초당 수 백 개의 문자를 빠르게 생성하도록 설계됐다.

쿠글러는 단계를 세부적으로 나눠 실험을 진행했다. 우선 첫 글자인 'T'를 찾는 데 걸린 시간과 문자 수를 기록했고, 이 절차를 10회 반복하여 평균적으로 걸리는 시간과 문자 수를 조사했다. 다음으로 이전 방식과 똑같이 'To'를 무작위로 생성하는 데 평균적으로 걸리는 시간을 기록했고 'To be'까지 생성해냈다.

아래 표에 나와있듯이 'T'를 생성하기 위해 약 60개의 문자를 무작위로 생성했으며 'To be'를 생성하기 위해 평균 3억4583만940개의 문자를 생성했다. 두 단어를 생성하는 데도 약 1100초나 걸렸다.

이 시점에서 커글러는 위기 의식을 느꼈다. 문장의 다음 문자를 올바르게 생성하는 데 필요한 시간을 감안했을 때, 이 작업이 인류가 멸망할 때까지 안 끝날 수 있다는 것을 깨달았기 때문이다. 따라서 커글러는 이전에 만든 데이터를 사용해 전체 문장을 생성하는 데 필요한 문자 수와 계산 시간을 추정했다.

쿠글러의 계산에 따르면, “To be, or not to be, that is the Question”를 완성하려면 약 2.69×10의 69제곱 개의 문자가 필요하며 이는 약 9.35×10의 58제곱 년이나 기다려야 하므로 엄청난 인내가 필요하다.

우주의 나이가 138억 년으로 추정되는데, 문장이 완성되려면 빅뱅 이후부터 지금까지의 시간에 7×10의 48제곱 배의 시간을 기다려야 한다. 그리고 이것은 햄릿의 겨우 ‘한 문장’을 만들어내는 데 불과한 시간이다. 현실은 시간이 무한하지 않다는 점에서 키케로의 가설이 맞았다. 유한한 시간 내에 문장을 읽을 수 있는 수준으로 우연히 만들 가능성은 매우 희박하다. 종합하여 무한 원숭이 정리는 '무한'이라는 개념이 인간이 상상하고 인지하는 수준보다 훨씬 크다는 것을 보여준다.

*편집진: 영어 원문의 출처는 사이언티픽 아메리칸(Scientific American)으로 본지의 편집 방향과 일치하지 않을 수도 있습니다.