표본 추출 편향으로 발생한 우정의 역설
부분적인 관점과 전체적인 관점의 차이에서 비롯
연구 대상이 특정 표본이면 무작위 표본 추출에도 역설 활용해

[해외DS]는 해외 유수의 데이터 사이언스 전문지들에서 전하는 업계 전문가들의 의견을 담았습니다. 저희 데이터 사이언스 경영 연구소 (GIAI R&D Korea)에서 콘텐츠 제휴가 진행 중입니다.

1991년 사회학자 스콧 펠드(Scott Feld)는 소셜 네트워크의 속성을 연구하던 중 놀라운 사실을 발견했다. 펠드는 네트워크에 속한 사람의 평균 친구 수를 계산한 후 이를 친구들의 평균 친구 수와 비교한 결과, 대다수의 친구 수는 평균적으로 친구들의 친구 수보다 적었다. 하지만 여기서 조금 이상한 점은 대다수의 친구 수가 평균적으로 더 적은데, 어떻게 주변 친구들의 친구 수가 평균적으로 더 많다는 사실이 서로 양립할 수 있는 걸까?

이를 '우정의 역설'(Friendship paradox) 또는 '친구의 역설'이라고 하며 더 일반적으로는 '조사의 역설'(Inspection paradox)이라고 부른다. 이러한 역설은 삶 곳곳에서 발견할 수 있는데, 기차나 버스를 평균적으로 더 오래 기다리는 것처럼 느껴지는 이유, 콜센터의 통화량이 항상 평균보다 많은 것처럼 느껴지는 이유 등을 예로들 수 있다. 결과적으로 보면 이는 통계학에서 말하는 표본 편향이 일으킨 오류다. 더 쉽게는 친구의 친구 수가 많으므로 상대적으로 친구가 적은 사람들이 많아지는 원리고, 평균적인 대기 시간보다 긴 대기 구간이 짧은 구간보다 실제로 더 많기 때문에 개인이 느끼는 기다림은 확률적으로 더 길었던 것이다. 당연한 얘기 같으면서도 헷갈리는 이 역설을 위에서 언급한 예시들로 하나하나 살펴보자.

우정의 역설, 소셜 네트워크의 글로벌 관점 vs. 국지적 관점

먼저 평균적으로 수백 명의 친구를 보유한 페이스북(현 메타)과 같은 소셜 네트워크를 생각해 보자. 10,000명의 친구를 가진 '인싸'는 10,000명의 다른 사용자의 친구 목록에 나타나기 때문에 평균적인 친구 수를 보유한 그의 많은 친구들은 상대적으로 인기가 없다고 느끼게 된다. 반대로 친구가 5명인 사용자는 5명의 친구 목록에만 나타나기 때문에 평균적인 친구 수를 보유한 5명만이 자신을 인기가 있다고 느낀다. 그 결과 인기가 없다고 느낀 사용자의 수가 인기가 높다고 느낀 사용자의 수보다 압도적으로 높을 수밖에 없는 것을 확인할 수 있다. 이에 따라 친구가 보유한 친구 수가 자신보다 항상 평균적으로 더 많다고 느꼈던 것이다.

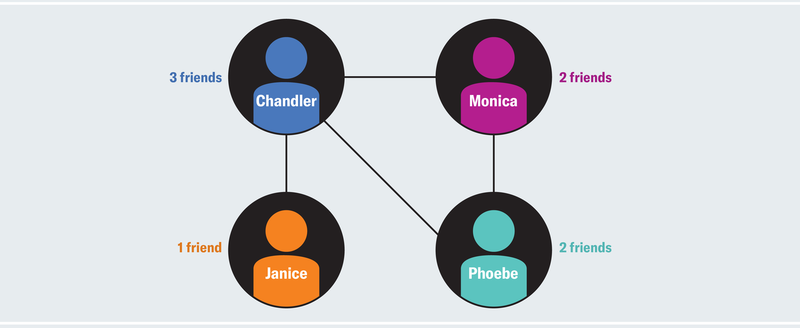
4명의 사용자가 총 8명의 친구를 보유한 네트워크가 있다. 챈들러는 친구가 3명, 모니카와 피비는 2명, 제니스는 1명으로, 4명의 평균 친구 수는 2명이며 모니카의 친구 수는 전체 네트워크의 평균과 같으므로 모니카는 친구가 많지도 적지도 않은 평범한 사용자에 속한다. 그러나 모니카가 친구를 맺은 챈들러와 피비가 보유한 친구 수의 평균은 (3 + 2) / 2 = 2.5명이다. 즉 모니카의 친구들은 평균적으로 모니카보다 더 많은 친구를 가지고 있으므로(2.5 > 2), 모니카는 실제로는 지극히 평균적인데도 불구하고 상대적으로 인기가 없다고 느낄 수 있다.

친구의 친구 수가 평균적으로 각각 2.5명과 3명인 피비와 제니스도 마찬가지다. 챈들러의 친구 그룹만 평균 1.67명의 친구를 보유하고 있어, 이 네트워크에 속한 대다수는 자신의 인기가 낮다고 평가하게 된다. 이를 다른 방식으로도 증명할 수 있는데, 친구의 평균 친구 수 (2.5 + 2.5 + 3 + 1.67) / 4 = 2.42와 평균적인 사람의 친구 수인 2를 비교해서 해당 네트워크의 대다수는 자신을 인기가 없다고 판단했음을 정량화할 수 있다. 모든 사람이 동일한 수의 친구를 가지고 있지 않은 한, 놀랍게도 이러한 현상은 모든 네트워크에서 항상 발생한다.

학급 규모 조사와 교통 대기 시간, "왜 나만 붐비고 오래 기다리지?"

우정의 역설이 다소 이해하기 어려웠어도 괜찮다. 다른 예를 보자. 대학생들에게 평균 학급 규모를 물어보면 학교 측에서 공식적으로 발표하는 평균 학급 규모보다 항상 더 큰 수치로 왜곡돼서 집계된다. 학생들이 과장하고 있는 걸까, 아니면 학생 대 교사 비율을 더 유리하게 보이게 하려고 학교 측에서 수치를 부풀린 것일까? 각자의 관점에서 보면 모두 맞는 말이다. 대규모 강의를 듣는 학생들은 당연히 평균 수업 규모가 더 크다고 보고하는 반면, 소규모 강의만 듣는 학생들은 평균 수업 규모가 더 작다고 보고할 것이다. 하지만 대규모 강의실에는 소규모 강의실보다 더 많은 사람이 수강할 수 있기 때문에 전자의 그룹에 훨씬 더 많은 사람이 속한다. 그래서 학생을 대상으로 한 설문조사에서는 등록률이 높은 수업이 등록률이 낮은 수업보다 더 자주 집계되는 반면, 대학에서 평균 수업 규모를 집계할 때는 대규모 강의와 소규모 강의를 각각 한 번씩만 집계하므로 학교와 학생이 생각하는 평균적인 학급 규모가 달랐던 것이다.

조사의 역설은 대중교통에서도 작동한다. 지하철 열차가 평균 8분마다 한 역에 정차한다고 가정하자. 출퇴근 시간을 제외하고 열차 사이의 임의의 시간에 역에 도착하면 7분 50초 동안 앉아있을 때도 있고, 개찰구를 통과할 때쯤 기차가 다가오는 소리가 들릴 때도 있을 것이다. 이런 경우 시간이 지나면서 평균적으로 4분 정도 기다리는 것으로 예상할 수 있다. 그런데 왜 항상 그보다 더 길게 느껴질까?

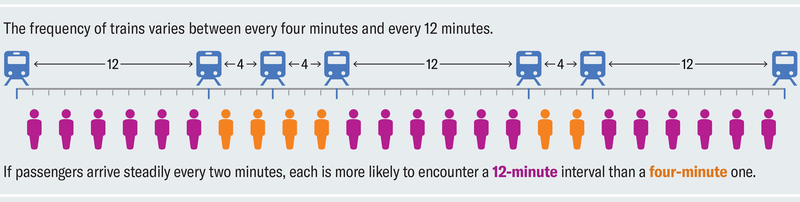
물론 평균 8분마다 기차가 도착한다고 해서 8분마다 정시 도착하는 것은 아니다. 배차 간격이 길기도 하고 짧기도 하는 등 일정이 엇갈리기도 한다. 하지만 학급 규모 조사와 마찬가지로 간격이 길기 때문에 긴 대기 시간을 경험한 사람이 더 많아진 것이다. 더 구체적으로는 6회의 배차 간격 중 절반은 12분, 나머지 절반은 4분인 배차 스케줄이 있을 때, 대중교통 당국은 열차 간 평균 배차 간격이 8분이라고 광고할 수 있지만, 개인 통근자들은 배차 간격이 길어져 불쾌한 대기를 경험할 확률이 3배나 높다.

역설의 재발견, 특정 표본에 관심 있을 때는 역으로 활용

이렇듯 사람의 직관과 통계가 부딪히는 분야에선 역설로 인해 발생할 수 있는 편향을 조심해야 한다. 연구의 방향과 결과 모두 영향을 받기 때문이다. 하지만 조사의 역설이 항상 연구에 방해가 되는 방식으로만 작동하지 않는다. 일부 영리한 연구자들은 무작위 표본 추출을 개선하기 위해 이 현상을 이용하기도 했다. 특히 흥미로운 예는 독감의 확산에 관한 연구에서 찾을 수 있다.

독감이 유행할 때 사회적 접촉이 많은 사람들은 질병에 더 일찍 걸리는 경향이 있다. 따라서 무작위로 독감 상태를 확인하는 순진한 방법으로는 사회적 접촉이 많은 사람들에게 우선순위를 부여할 수 없고, 소셜 네트워크의 전체적인 구조를 파악하는 데도 너무 많은 시간이 소요된다. 이때 연구자들은 무작위로 사람들을 골라 그들의 친구를 모니터링하는 방법을 시도했다. 앞서 살펴본 바와 같이, 대다수 사람들의 친구는 자신보다 더 인기 있는 경향이 있어서 이러한 약간의 조정으로 사회적 접촉이 많은 사람들이 표본에 나타날 확률을 크게 높일 수 있다. 이 기법을 통해 연구진은 기존의 무작위 표본 추출 방식보다 2주 일찍 독감 발병을 감지할 수 있었다.

연구 분야에서 일하지 않는 다른 사람들에게도 조사의 역설은 일상적인 관찰을 설명하는 데 도움이 될 수 있다. 적어도 자신이 불운하다는 생각에서 잠시 벗어날 기회를 얻을 수 있다. 콜센터의 통화량이 항상 평소보다 많은 것처럼 느껴질 때, 직원의 인력 부족을 탓하는 대표의 얼굴을 떠올리기 전에 좀 더 넓은 시야를 가져보자. 어쩌면 우리가 큰 규모의 동시 통화자 그룹에 속했고, 동시 통화자 그룹이 일반적으로 더 크기 때문에 대기시간이 길어졌을 가능성이 높다. 가끔 운이 나쁘다고 느낄 때는 '나'(부분)에서 '우리'(전체)의 관점으로 생각을 확장해 보자.

영어 원문 기사는 사이언티픽 아메리칸에 게재되었습니다.